Fix the mass and the spring; i.e., let mass \(m\) and the spring constant \(k\) be fixed.
For different values of the damping coefficient \(\gamma\), the resulting vibrations will behave differently, in particular, will have different decay rates.
In the following, fix \(m=\frac{1}{2},k=8\), and consider different values of \(\gamma\).
| The Diff Eq | Eigenvalues | |
|---|---|---|
| \(\displaystyle m\frac{d^2 y}{dt^2} +\gamma\frac{dy}{dt} +ky =0 \) | \(\displaystyle \lambda=\frac{-\gamma\pm \sqrt{\gamma^2-4mk} }{2m} \) | |
| \(\displaystyle \frac{1}{2}\frac{d^2 y}{dt^2} +\gamma\frac{dy}{dt} +8y =0 \) | \(\lambda=-\gamma\pm \sqrt{\gamma^2-16}\) |
The mass and the spring constant are fixed: \(m=\frac{1}{2},k=8\).
The values of the damping coefficients are: \(\gamma=0,1,4,7\).
| Type of Damping | Conditions | Eigenvalues | Solution Behavior | Examples |
|---|---|---|---|---|
| No damping | \(\gamma=0\) | \(\begin{array}{l} \mbox{Purely imaginary:}\\[0.5ex] \lambda_{1,2}=\pm i \sqrt{\frac{k}{m}} \end{array}\) |
Periodic Oscillation
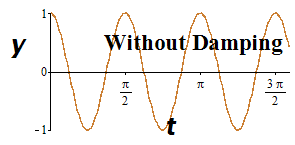
| \(\begin{array}{l} m=\frac{1}{2},k=8,\gamma=0.\\[0.5ex] \frac{1}{2}\frac{d^2 y}{dt^2} +8y =0\\[0.5ex] y(t)=C_1\cos(4t)+C_2\sin(4t)\\[0.5ex] \mbox{No Decay.} \end{array}\) |
| Under-damping | \(\begin{array}{l} \gamma>0,\\[0.5ex] \gamma^2-4mk<0 \end{array}\) | \(\begin{array}{l} \mbox{Complex eigenvalues}\\[0.5ex] \mbox{with } \mbox{Re}\,\left(\lambda_{1,2}\right)<0 \end{array}\) |
Oscillatory decay
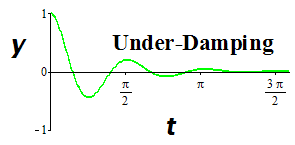
|
\(\begin{array}{l} m=\frac{1}{2},k=8,\gamma=1.\\[0.5ex] \frac{1}{2}\frac{d^2 y}{dt^2} +\frac{dy}{dt} +8y =0\\[0.5ex] y(t)=e^{-t}[C_1\cos(\sqrt{15}\ t)+C_2\sin(\sqrt{15}\ t)]\\[0.5ex] \mbox{Decay Rate: \(-1\)} \end{array}\) |
| Critical-damping | \(\begin{array}{l} \gamma>0,\\[0.5ex] \gamma^2-4mk=0 \end{array}\) | \(\begin{array}{l} \mbox{Repeated, real: }\\[0.5ex] \lambda_{1}=\lambda_{2}<0 \end{array}\) |
Monotonic Decay
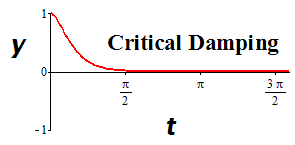
|
\(\begin{array}{l} m=\frac{1}{2},k=8,\gamma=4.\\[0.5ex] \frac{1}{2}\frac{d^2 y}{dt^2} +4\frac{dy}{dt} +8y =0\\[0.5ex] y(t)=C_1 e^{-4t}+C_2 te^{-4t}\\[0.5ex] \mbox{Decay Rate: \(-4\)} \end{array}\) |
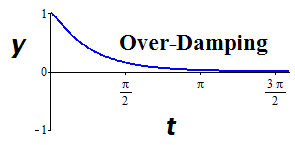
| Over-damping | \(\begin{array}{l} \gamma>0,\\[0.5ex] \gamma^2-4mk>0 \end{array}\) | \(\begin{array}{l} \mbox{Distinct, real:}\\[0.5ex] \lambda_{1}<0,\lambda_{2}<0 \end{array}\) |
Monotonic Decay
|
\(\begin{array}{l} m=\frac{1}{2},k=8,\gamma=7.\\[0.5ex] \frac{1}{2}\frac{d^2 y}{dt^2} +7\frac{dy}{dt} +8y =0\\[0.5ex] y(t)=C_1 e^{(-7+\sqrt{33})t}+C_2 e^{(-7-\sqrt{33})t}\\[0.5ex] \mbox{Decay Rate: } \lambda_1=-7+\sqrt{33}\approx -1.26 \end{array}\) |
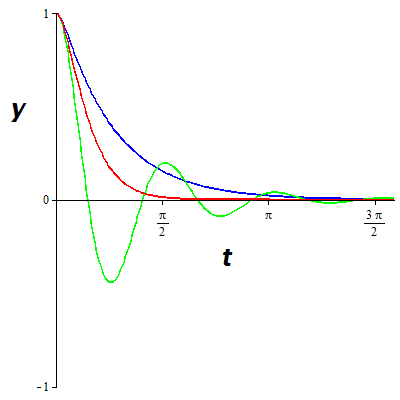
Critical Damping (red), Under-Damping (green), and Over-Damping (blue).
QUESTION:
Compare the three graphs. Which one decays fastest?